二元搜尋樹(Binary Search Tree)

Da-Wei Chiang

大綱

  • 何謂二元樹
  • 圖例二元樹
    • 二元樹的結構
    • 二元樹的建構過程
    • 二元樹刪除節點過程
    • 特殊的二元樹
  • 實作練習

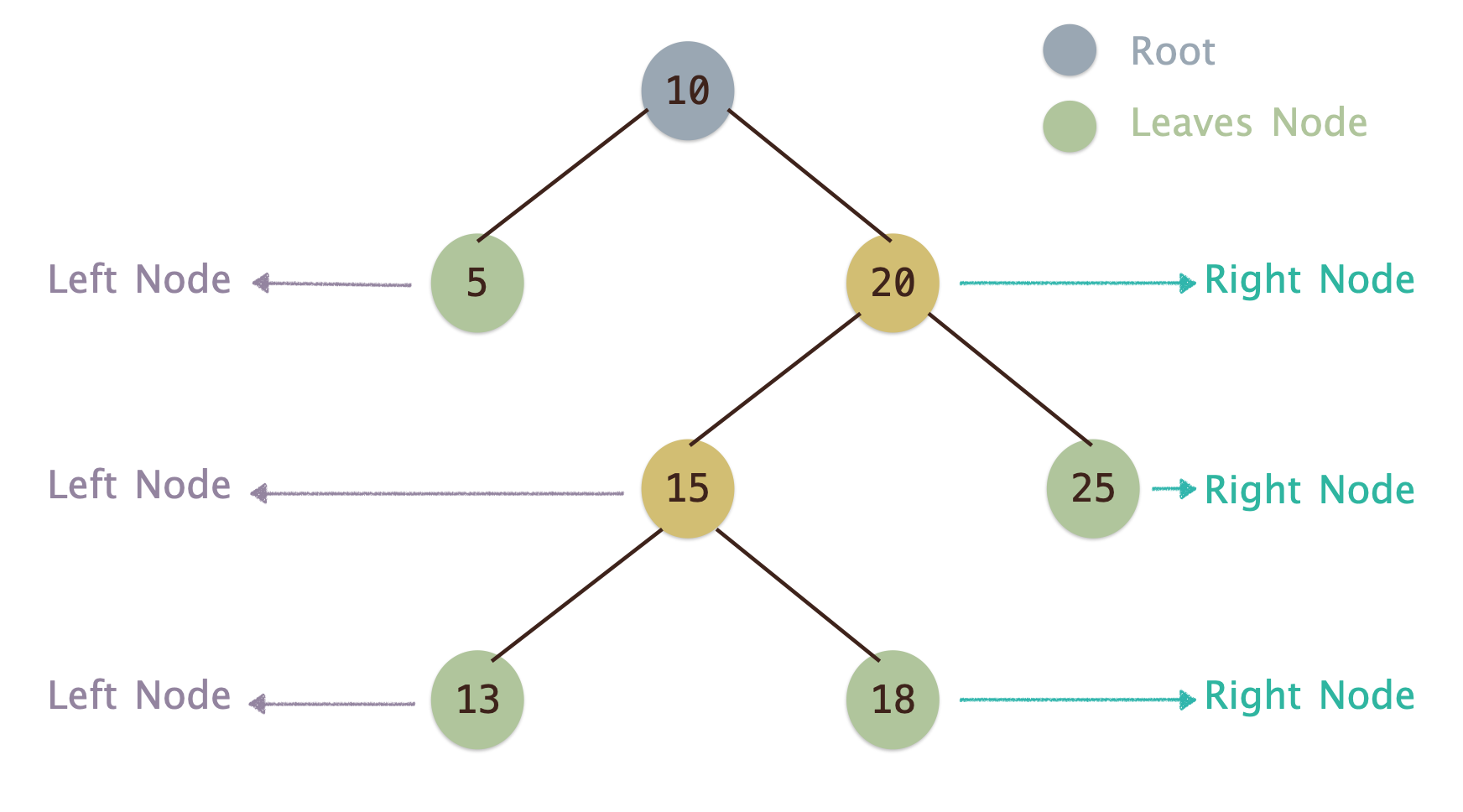
何謂二元樹

  • 二元樹是一種樹狀結構, 每個節點下最多只有兩個子節點.分別為左節點(Left Node)與右節點(Right Node)
  • 樹的最上方稱為根節點(Root)
  • 一棵樹下沒有任何子節點的節點稱為葉節點(Leaves Node)

二元樹的結構

二元搜尋樹的建構過程

  • 二元搜尋樹的建立規則
    • 若比當前節點大則往右走, 否則往左走
  • 假定有一組數分別為15, 8, 20, 19, 17, 25, 40要如何建構二元搜尋樹？
  • 首先以15為Root

二元搜尋樹的建構過程

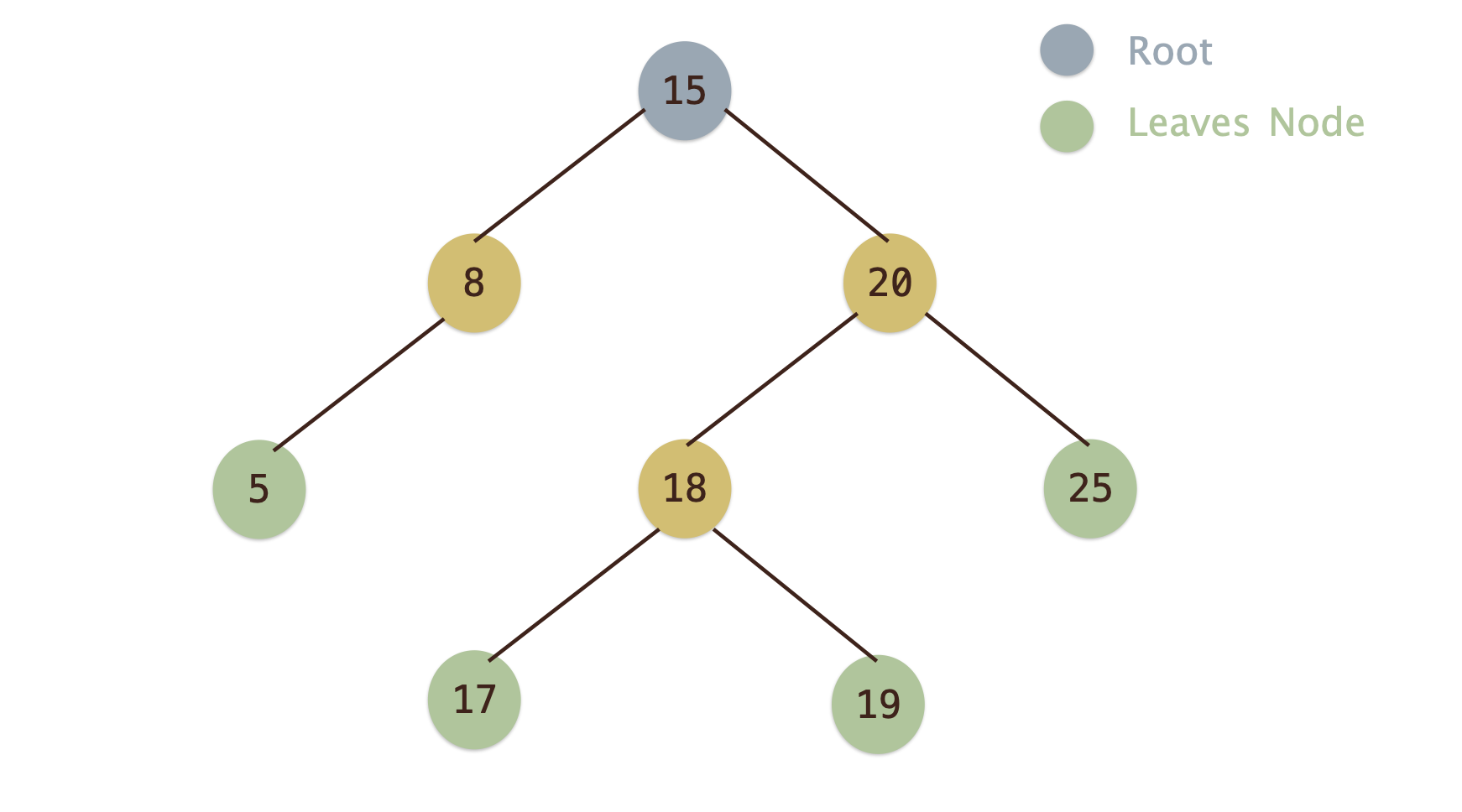
  • 假定有一組數分別為15, 8, 20, 18, 17, 25, 19, 5要如何建構二元搜尋樹？
  • 建構Root之後, 開始建構子節點
    • 8比15小往左走
    • 20比15大往右走
    • 18比15大往右走, 比20小往左走
    • 17比15大往右走, 比20小往左走、比18小往左走
    • 25比15大往右走, 比20大往右走
    • 19比15大往右走, 比20小往左走、比18大往右走
    • 5比15小往左走, 比8小往左走

實作練習

  • 建構二元樹
    • 陣列形式
    • 鏈結串列形式

建構二元搜尋樹

  • 實務上建構二元搜尋樹有兩種形式
    • 陣列建構二元樹
    • 鏈結串列建構二元樹

陣列建構二元搜尋樹(一)

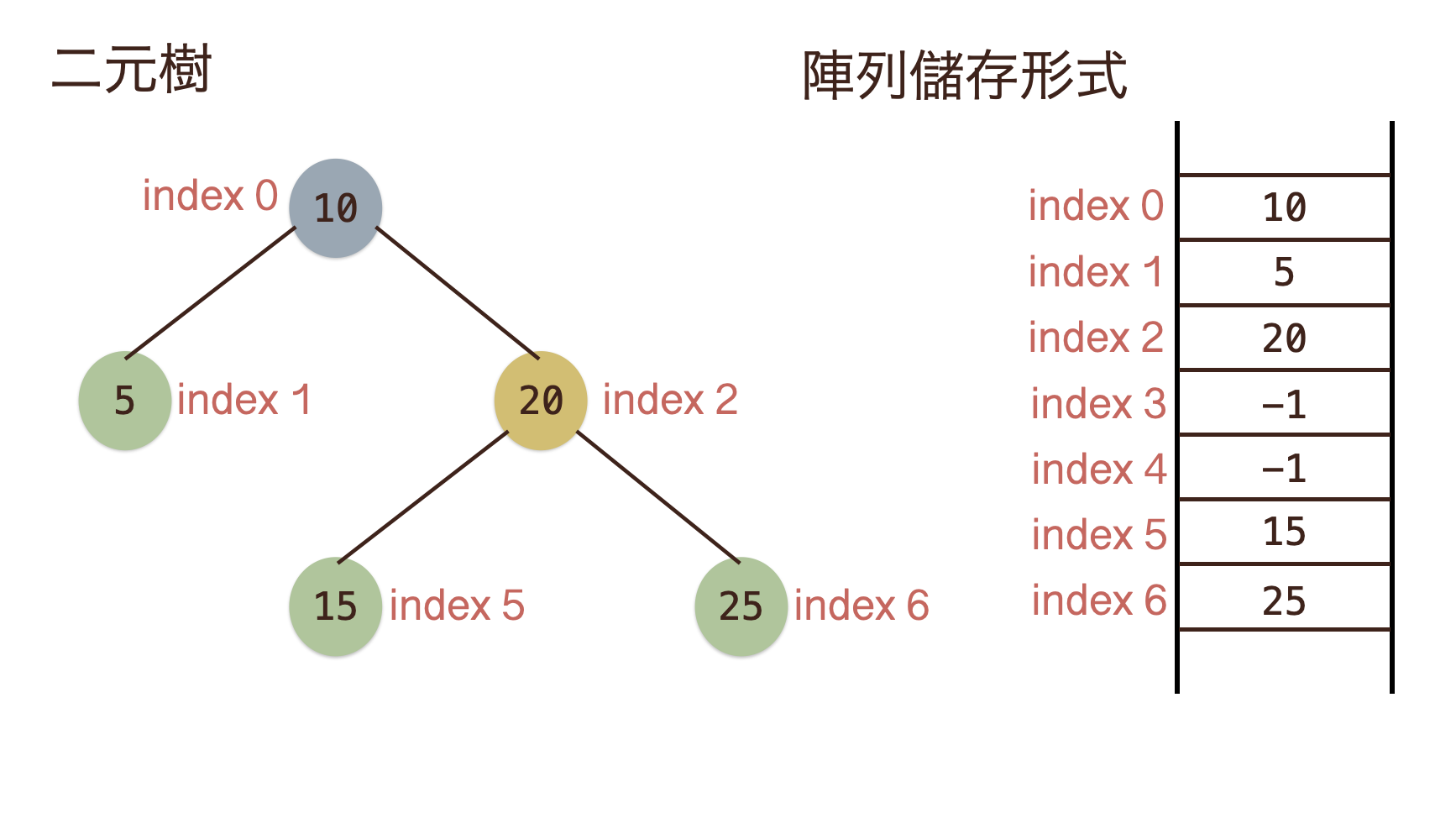
  • 我們知道陣列的儲存形式是一個連續的記憶體空間.
  • 在實務上如何透過陣列來儲存二元搜尋樹？如下圖所示

陣列建構二元搜尋樹(二)

  • 在實務上如何知道節點的左節點與右節點為何？如下圖所示

練習

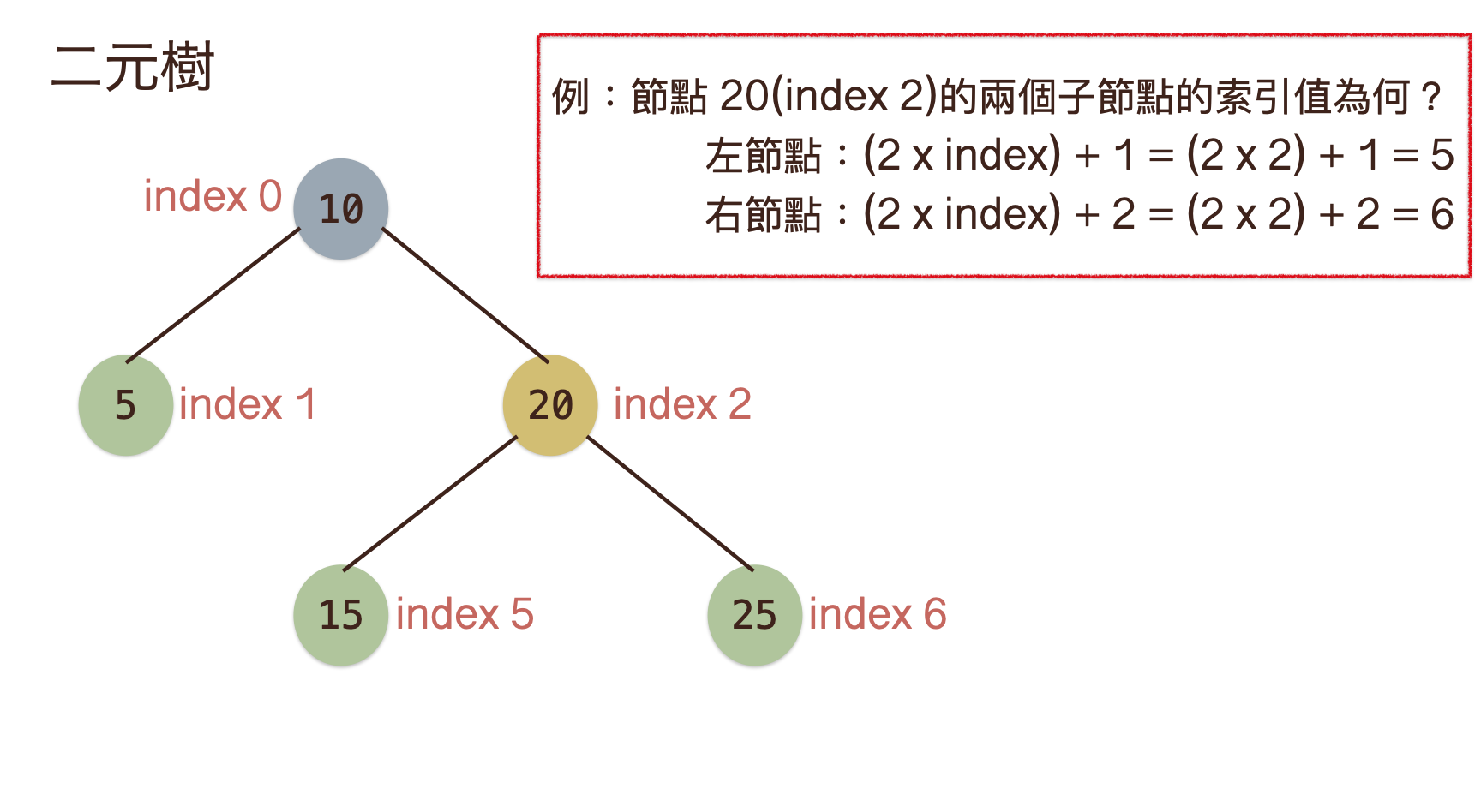
  • 使用python內建的list模擬儲存二元搜尋樹
    • 假定有一組數存在list中為[10, 20, 25, 15, 5]
    • 請撰寫程式模擬二元樹儲存於array的結果[10, 5, 20, -1, -1, 15, 25]共7個元素

請想想, 透過array儲存二元搜尋樹的優缺點為何？

練習

  • 請嘗試建立二元搜尋樹的類別.其建構子包含資料、左節點、右節點, 並建立物件印出該節點的資料

練習

  • 使用鏈結串列的技巧撰寫一個建立二元樹的方法建立二元搜尋樹
  • 將list中的數字[10, 20, 25, 15, 5] 建構至二元搜尋樹中(可先不印出結果)

PS:需使用到遞迴技巧

特殊的二元樹

  • 完滿二元樹(Full Binary Tree)
  • 完全二元樹(Complete Binary Tree)
  • 完美二元樹(Perfect Binary Tree)
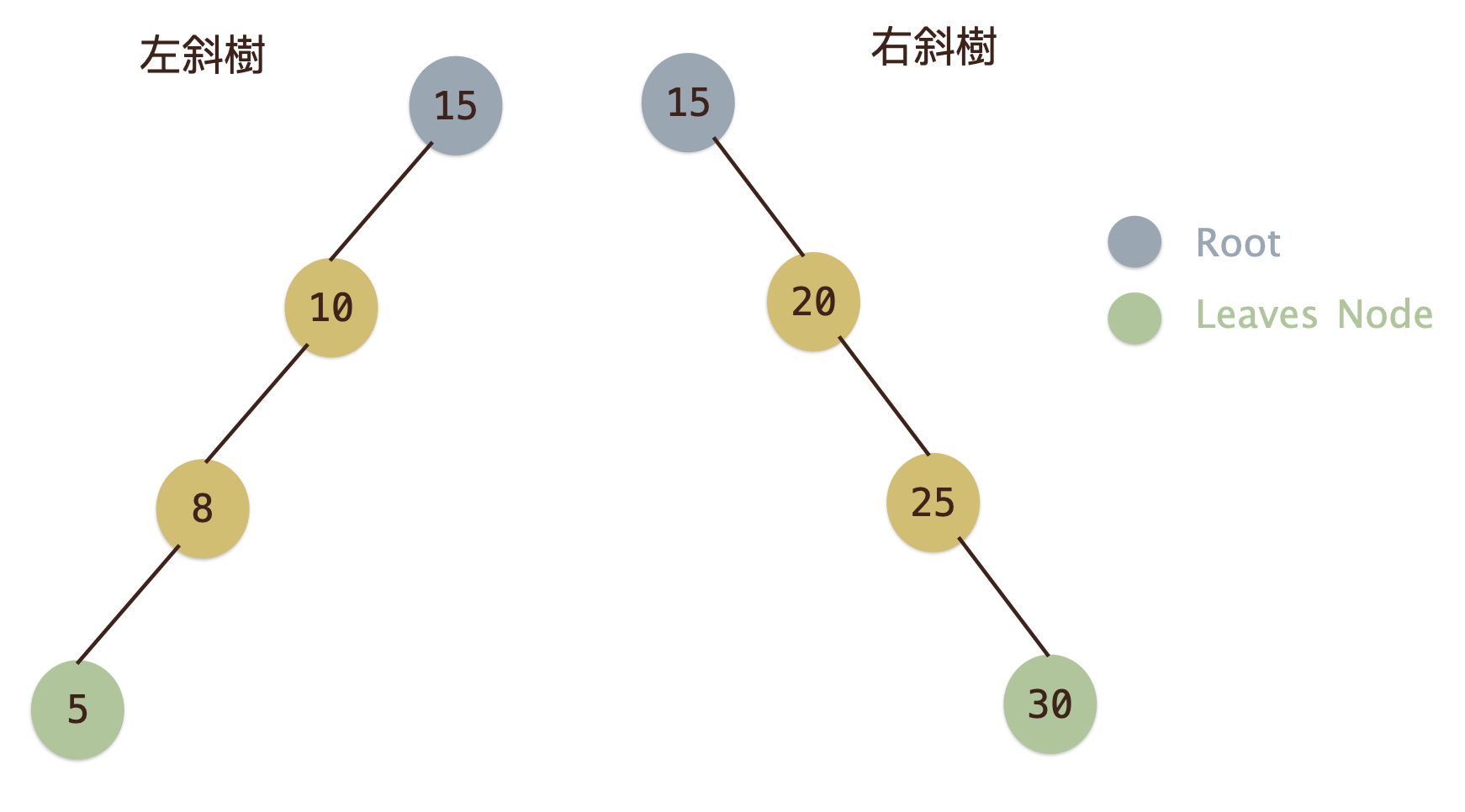
  • 歪斜樹(Skewed Tree)
    • 左斜樹(Left Skewed Tree)
    • 右斜樹(Right Skewed Tree)

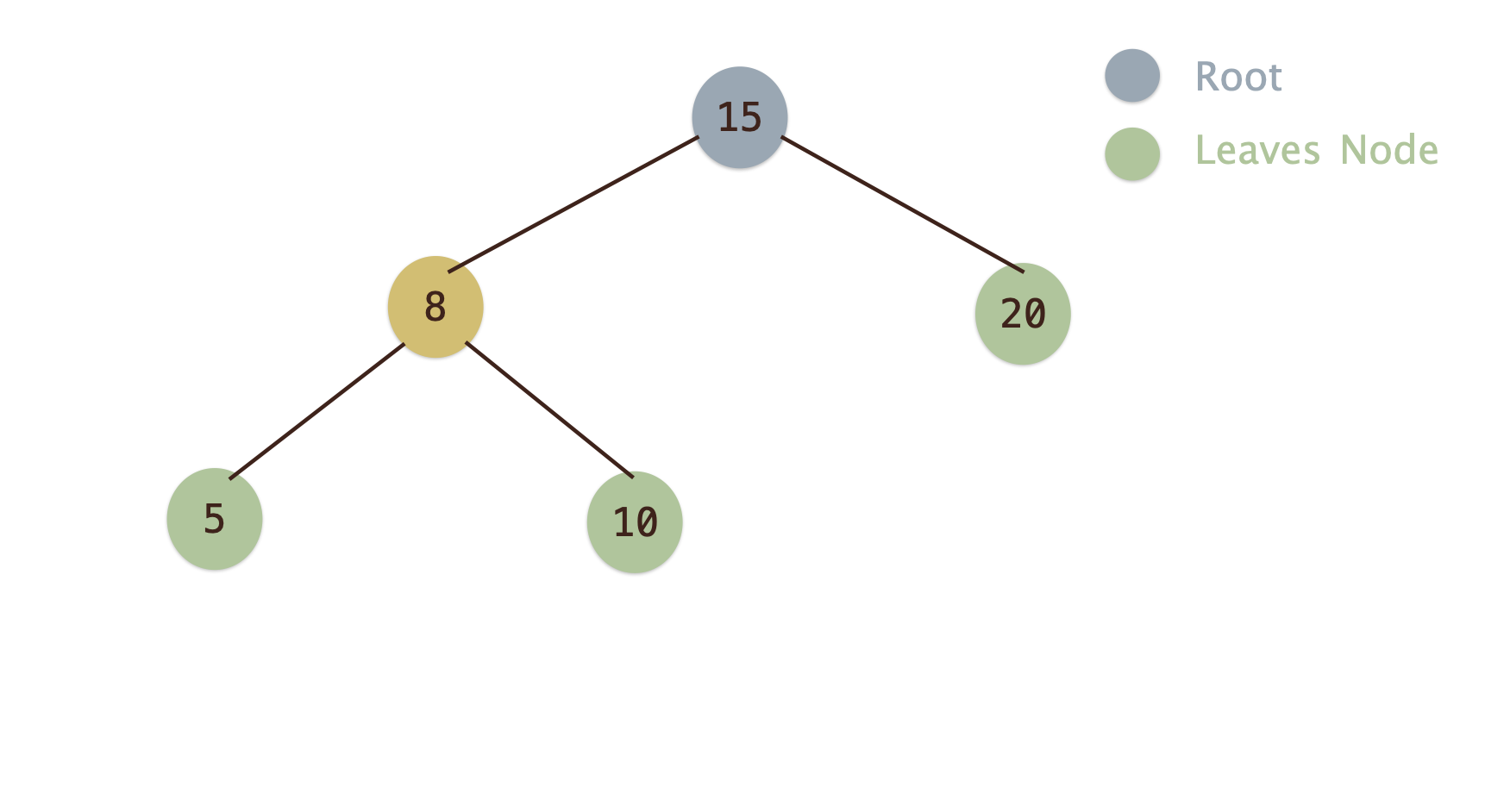
完滿二元樹(Full Binary Tree)

  • 除了葉節點之外, 每個節點均有兩個子節點
  • 第h層「最多」只有$2^{h-1}$個節點
    • 例：第三層最多只有$2^{3-1}=4$個節點

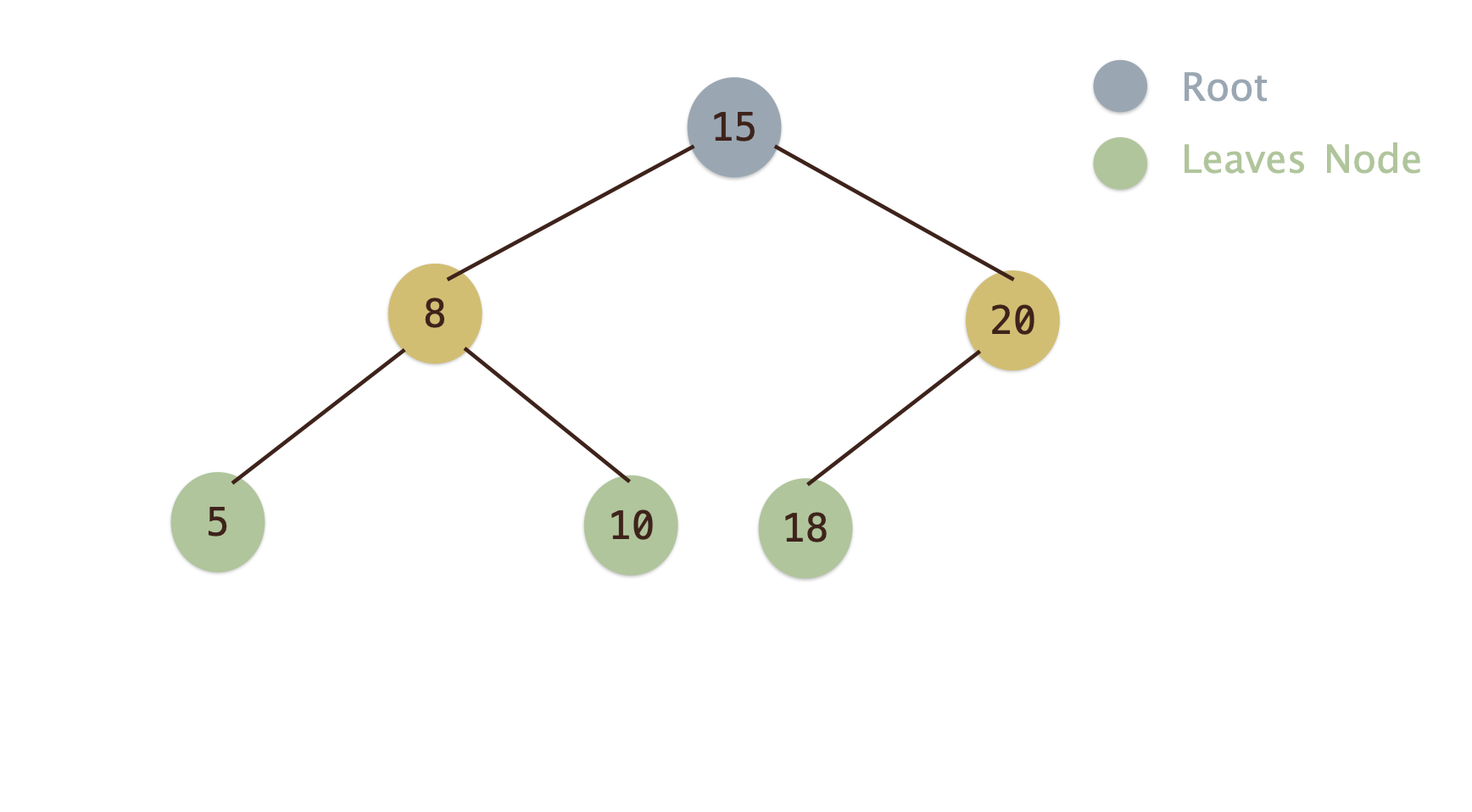
完全二元樹(Complete Binary Tree)

  • 除了葉節點之外, 每一層的節點均是滿的且最後一層的最後一個節點左邊的節點均是滿的

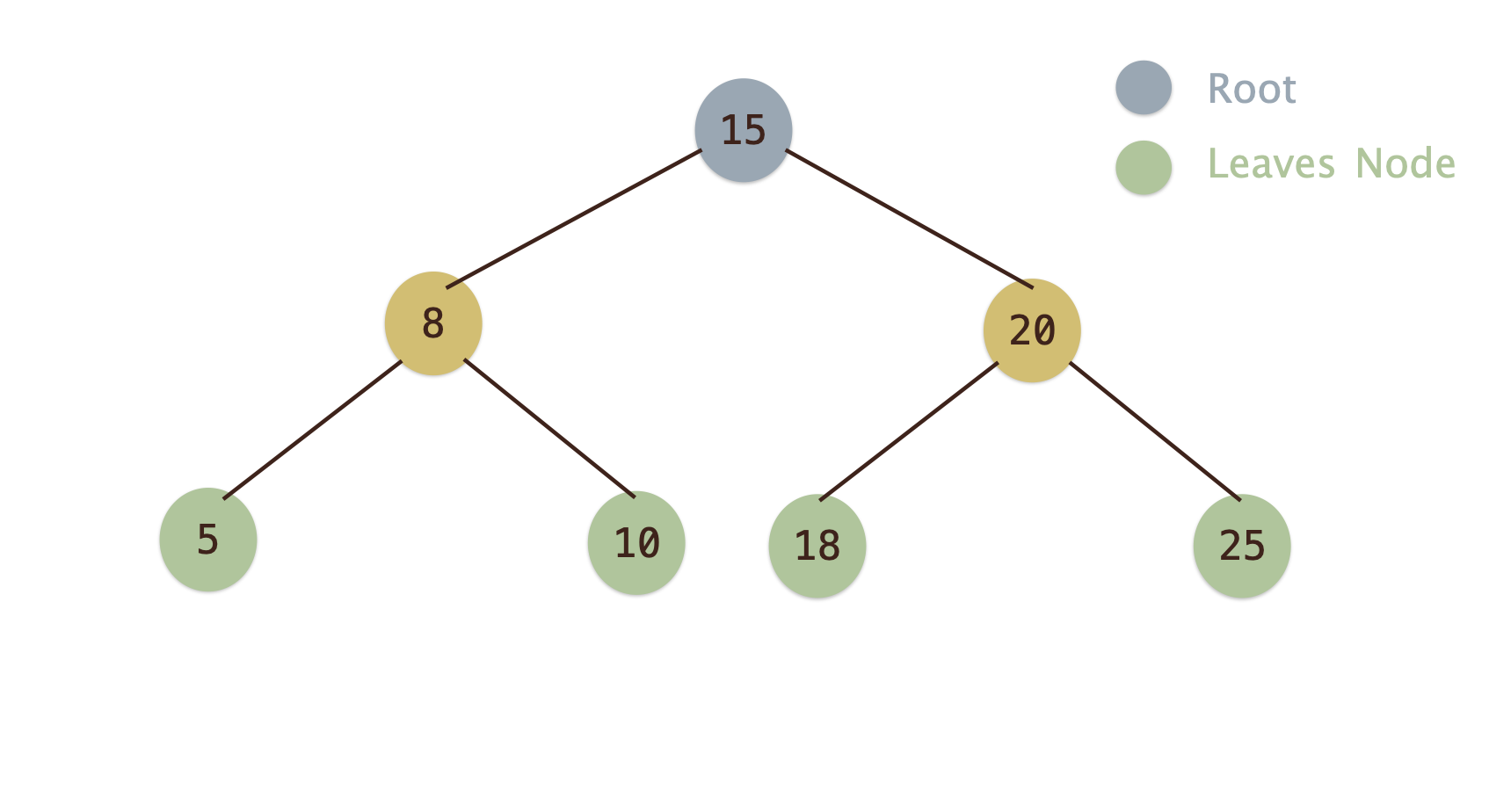
完美二元樹(Perfect Binary Tree)

  • 除了葉節點之外, 每一層的節點均是滿的.
  • 「完美二元樹」同時也是「完滿二元樹」與「完全二元樹」
  • 一顆完美二元樹有幾個節點？
    • 假定這顆完美二元樹的深度為h, 則這棵樹共有$2^h-1$個節點.
    • 例：如下圖共三層. 故共有$2^3-1=7$個節點

歪斜樹(Skewed Tree)

走訪二元樹

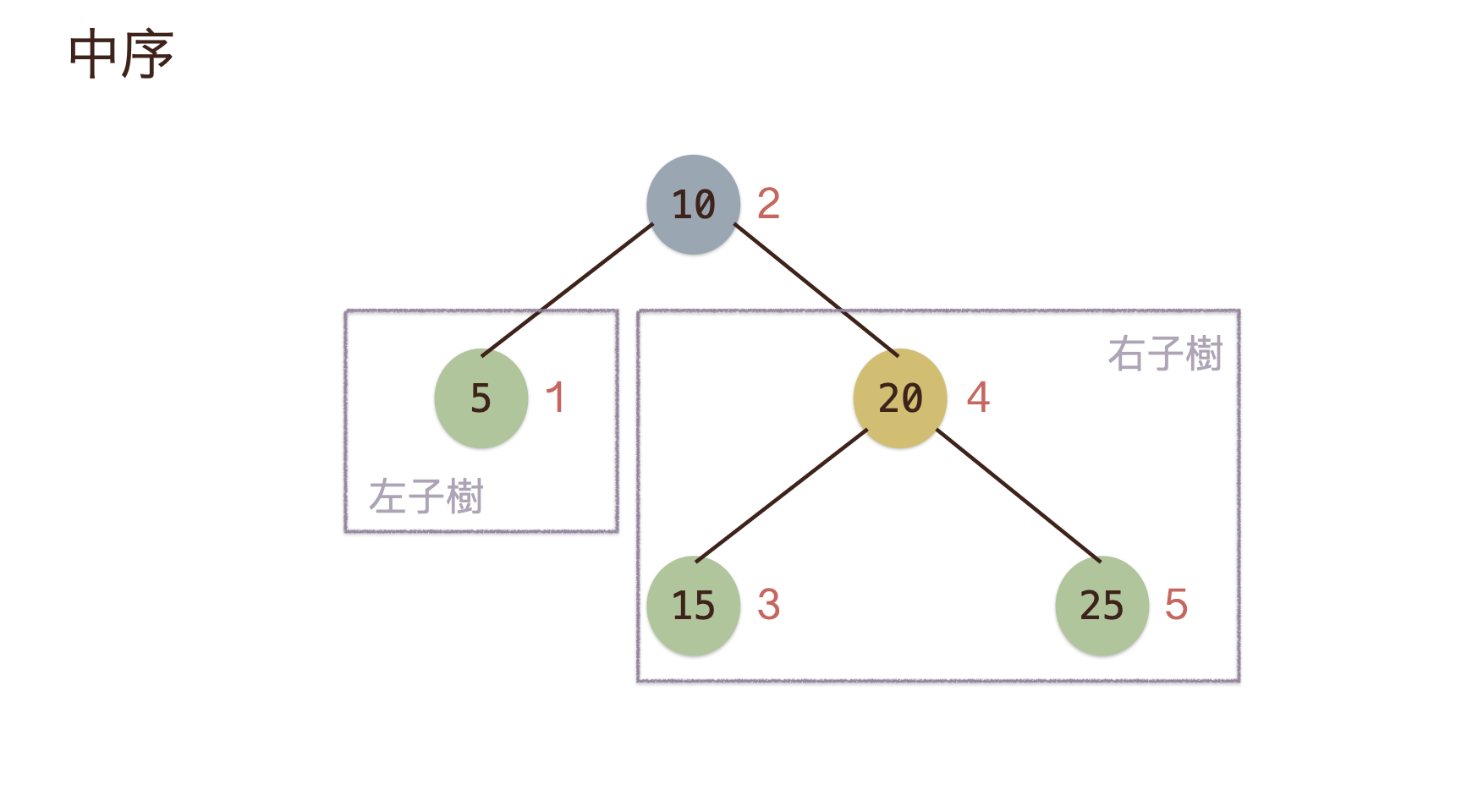
  • 中序(InOrder)
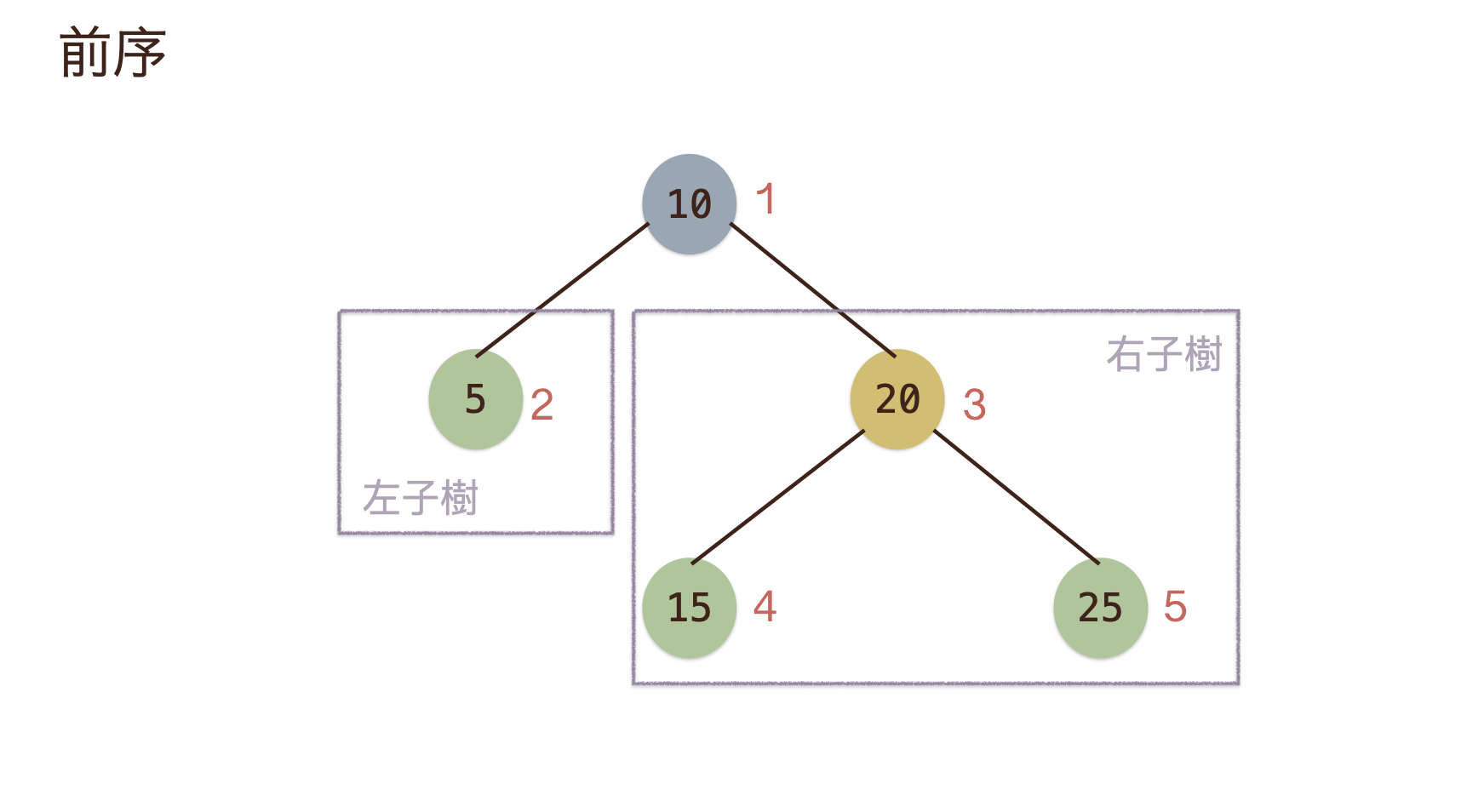
  • 前序(PreOrder)
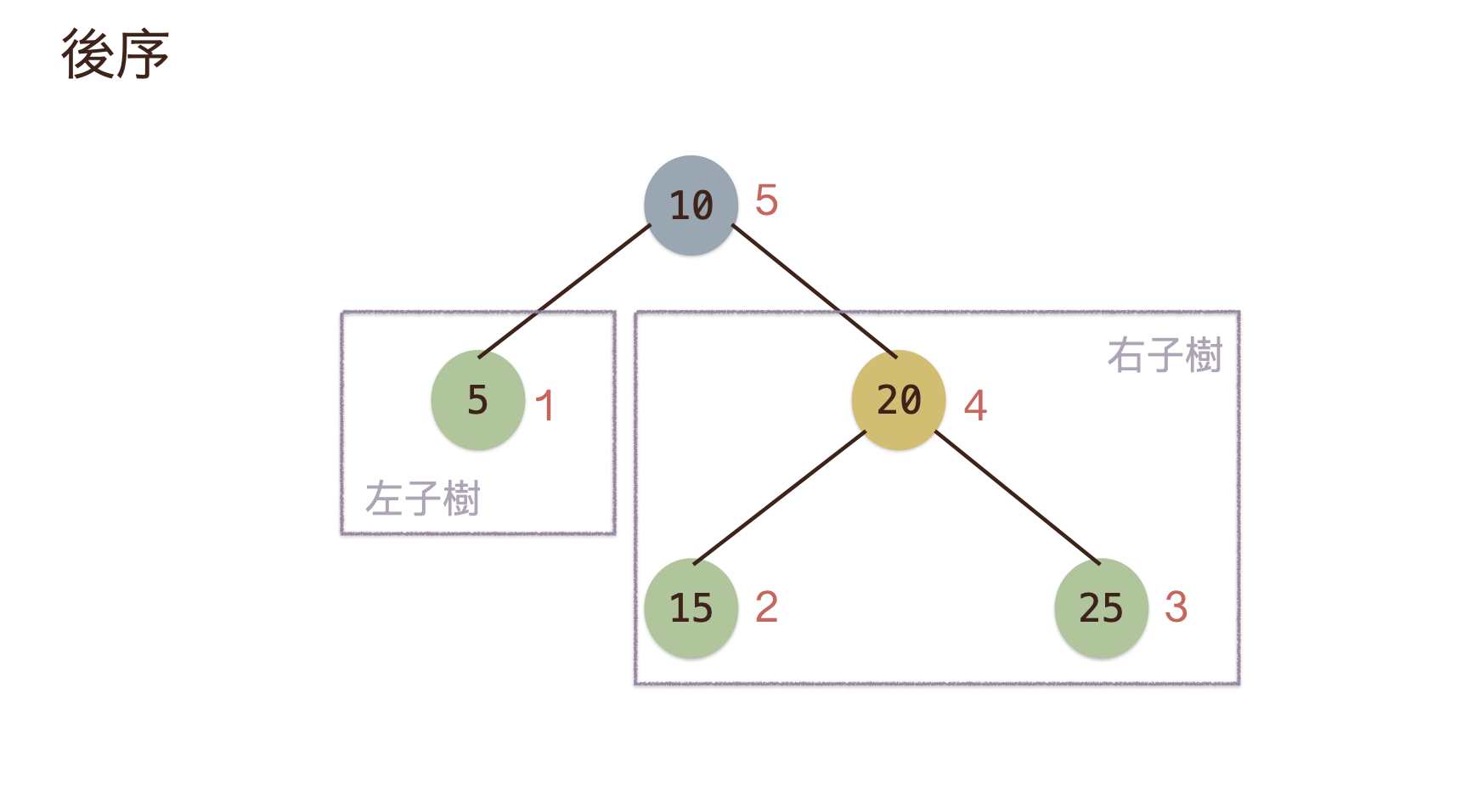
  • 後序(PostOrder)

中序(InOrder)

  • 走訪順序：左子樹 -> 根節點 -> 右子樹

練習

  • 承上題練習題
    • 使用鏈結串列的技巧撰寫一個建立二元搜尋樹的方法建立二元搜尋樹
    • 將list中的數字[10, 20, 25, 15, 5] 建構至二元搜尋樹中(可先不印出結果)
  • 撰寫一個中序的方法, 印出二元樹結構中的資料

前序(PreOrder)

  • 走訪順序：根節點 -> 左子樹 -> 右子樹

練習

  • 承上題練習題
    • 使用鏈結串列的技巧撰寫一個建立二元搜尋樹的方法建立二元樹
    • 將list中的數字[10, 20, 25, 15, 5] 建構至二元搜尋樹中(可先不印出結果)
  • 撰寫一個前序的方法, 印出二元樹結構中的資料

後序(PostOrder)

  • 走訪順序：左子樹 -> 右子樹 -> 根節點

練習

  • 承上題練習題
    • 使用鏈結串列的技巧撰寫一個建立二元搜尋樹的方法建立二元搜尋樹
    • 將list中的數字[10, 20, 25, 15, 5] 建構至二元搜尋樹中(可先不印出結果)
  • 撰寫一個後序的方法, 印出二元樹結構中的資料

二元搜尋樹刪除節點過程

  • 刪除二元樹節點有三種情況
    • 刪除的節點為葉節點
    • 刪除節點為非葉節點, 且此節點有一個子節點
    • 刪除節點為非葉節點, 且此節點有兩個子節點

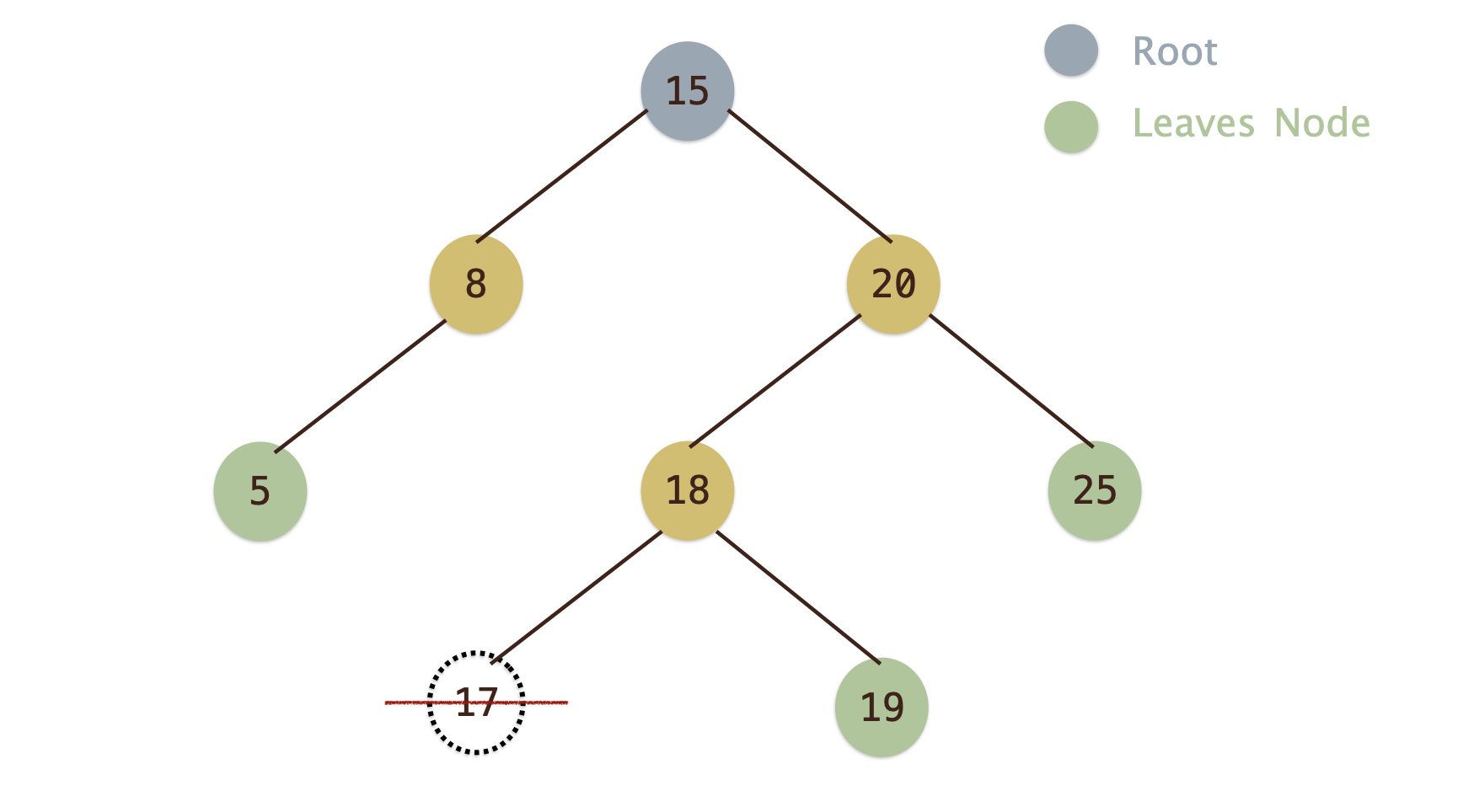
刪除的節點為葉節點

  • 若刪除節點為葉節點, 則直接刪除該節點即可
  • 如刪除節點17

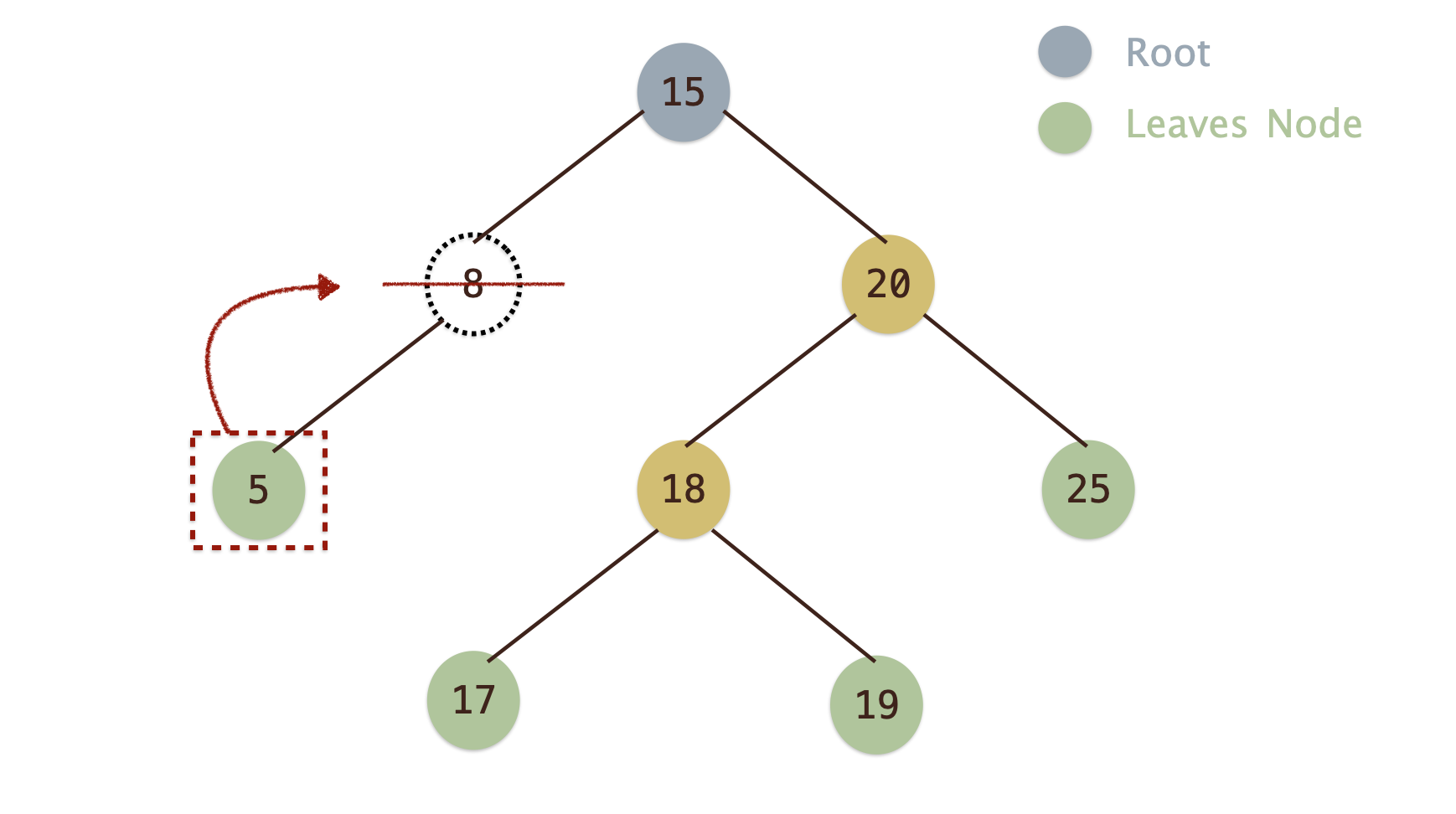
刪除節點為非葉節點, 且此節點有一個子節點

  • 若刪除節點為非葉節點, 且此節點有一個子節點, 則刪除完後將該子節點移至刪除節點位置
  • 如刪除節點8, 則將節點5移至節點8的位置

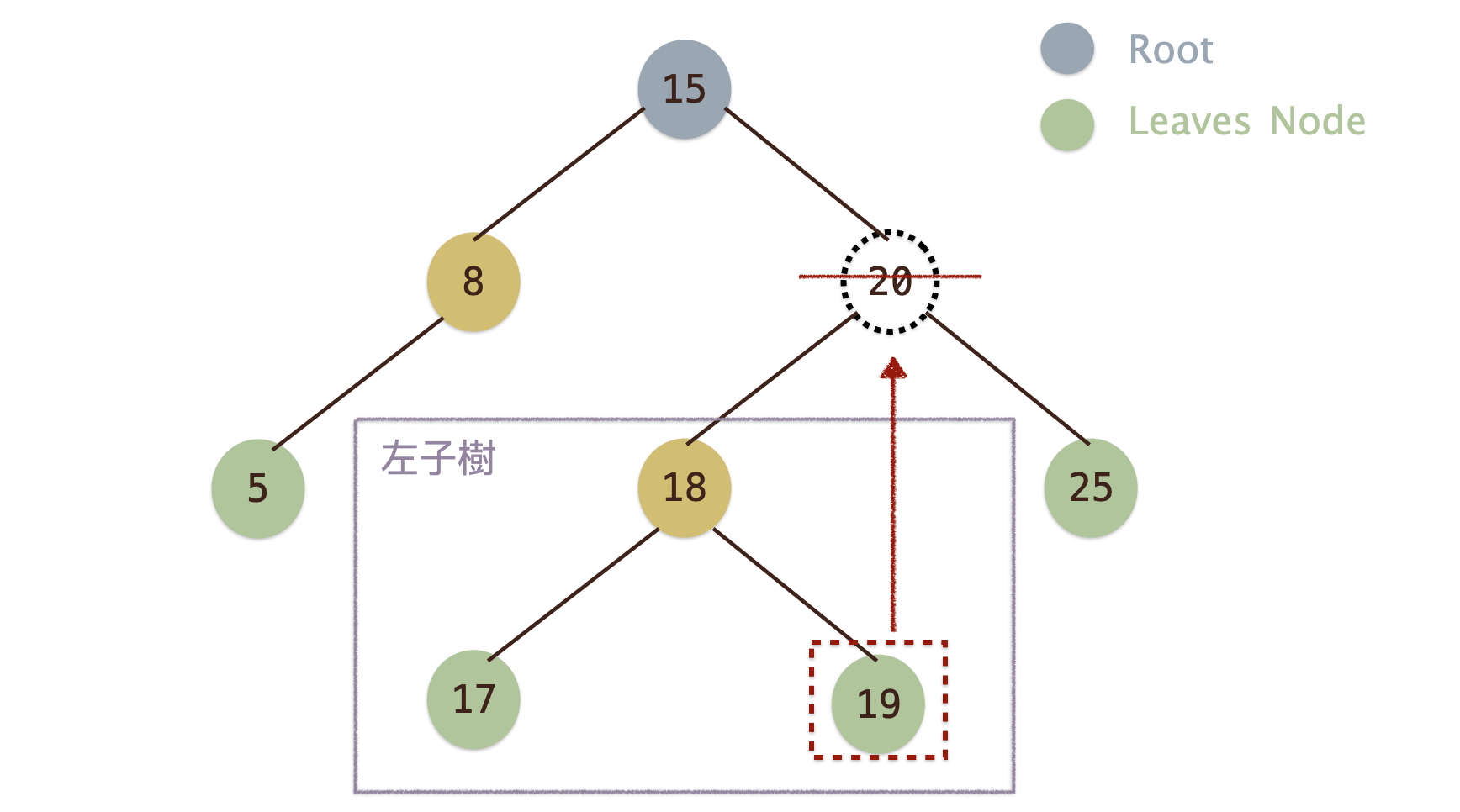
刪除節點為非葉節點, 且此節點有兩個子節點(一)

  • 若刪除節點為非葉節點, 且此節點有兩個子節點, 則有以下兩種做法
    1. 從預刪除節點的左子樹找出最大的節點移至刪除節點的位置. 若移動的節點也擁有兩個子節點則不斷重複該動作
    2. 從預刪除節點的右子樹找出最小的節點移至刪除節點的位置. 若移動的節點也擁有兩個子節點則不斷重複該動作
  • 作法1, 如要刪除20, 則從左子樹中找尋最大節點19移至節點20的位置

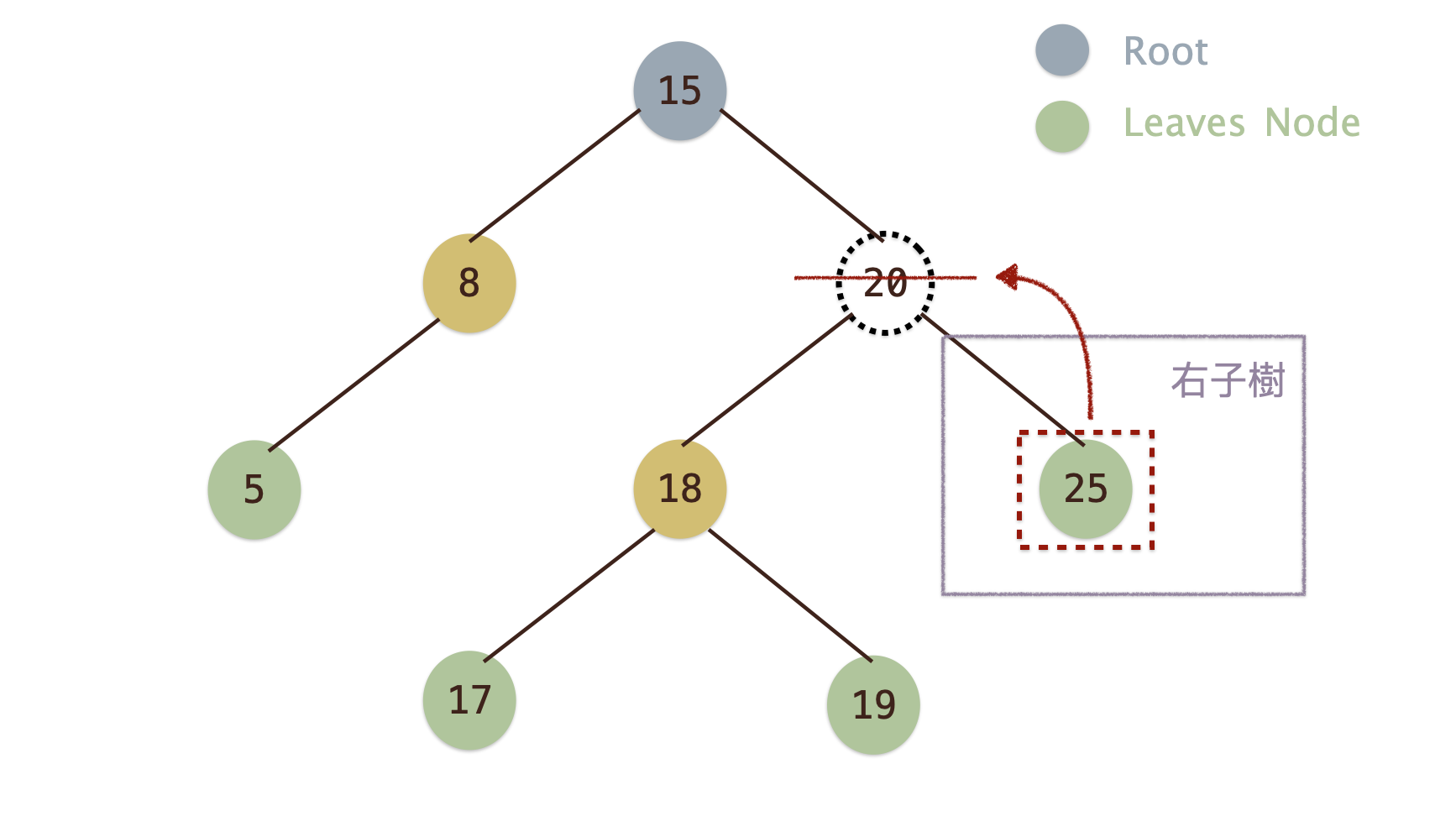
刪除節點為非葉節點, 且此節點有兩個子節點(一)

  • 若刪除節點為非葉節點, 且此節點有兩個子節點, 則有以下兩種做法
    1. 從預刪除節點的左子樹找出最大的節點移至刪除節點的位置. 若移動的節點也擁有兩個子節點則不斷重複該動作
    2. 從預刪除節點的右子樹找出最小的節點移至刪除節點的位置. 若移動的節點也擁有兩個子節點則不斷重複該動作
  • 作法2, 如要刪除20, 則從右子樹中找尋最小節點25移至節點20的位置

練習

  • 承上題練習題
    • 使用鏈結串列的技巧撰寫一個建立二元搜尋樹的方法建立二元搜尋樹
    • 將list中的數字[10, 20, 25, 15, 5] 建構至二元搜尋樹中(可先不印出結果)
    • 可使用前序、中序、後序的方法呈現結果
  • 撰寫一個類別Delete_Binary_Tree, 該類別帶入兩個參數如下.
    1. 準備要刪除節點的二元搜尋樹
    2. 要刪除的節點值
  • 於Delete_Binary_Tree類別中撰寫刪除節點的方法. 可確實刪除節點資料